✅ 그래프의 개념
- 노드(vertex) 와 간선(edge)을 이용한 비선형 자료구조
- 목적에 따라 간선의 가중치나 방향이 있을 수 있음

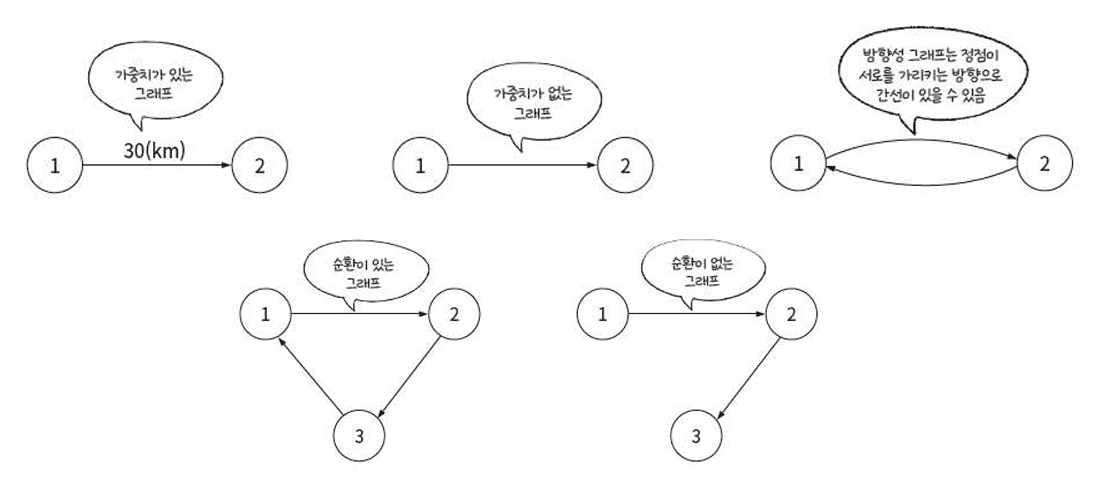
✅ 그래프의 종류
- 방향성, 가중치, 순환 특성에 따라 종류 구분
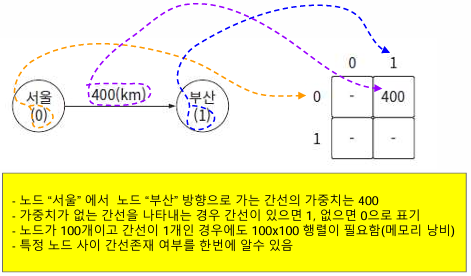
✅ 그래프의 구현 - 인접 행렬
- 행과 열의 인덱스로 노드의 값을 나타내고, 배열의 값은 간선의 가중치가 됨
- 노드 대비 간선이 적을 경우 메모리 공간 효율이 좋지 않음
✅ 그래프의 구현 - 인접 리스트
- 특정 시작 노드를 기준으로 연결된 노드들을 리스트로 연결하는 방식
- 실제 그래프의 노드 갯수만큼만 추가하므로 메모리 낭비 없음
- 특정 노드에 모든 노드가 연결된 경우, 탐색시 O(N) 이 될 수도 있음 (드문 케이스)
- 인접리스트 그래프 표현 방식
- 적절한 노드 정의 - 값(v) , 가중치(w), 노드 (next) 를 묶어서 관리
- 노드 개수 만큼 배열 준비 (각 배열 인덱스는 시작 노드 의미)
- 각 배열의 인덱스는 시작 노드를 나타냄, 해당 인덱스에 연결된 노드 추가
✅ 인접 행렬 vs 인접 리스트
| 공간 복잡도 | 특정 정점의 간선을 찾는 경우 | 그래프의 모든 간선을 찾는 경우 | |
| 인접 행렬 | O(V^2) | O(1) | O(V^2) |
| 인접 리스트 | O(V+E) | O(E) 대부분은 O(E/V) |
O(V+E) |
- 노드의 개수가 많을 때는 인접 리스트를 써야 함(인접행렬 사용시 메모리 초과 가능성)
- 특정 정점의 간선을 찾는 경우가 많으면 인접 행렬 사용 고려도 괜찮음
- 뭘 써야 할 지 모른다면 인접 리스트
✅ 그래프의 탐색
- 깊이 우선 탐색(DFS)
- 더 이상 탐색할 노드가 없을 때 까지 일단 간다.
- 더 이상 탐색할 노드가 없으면 최근에 방문했던 퇴각 후, 가지 않은 노드 방문
- 너비 우선 탐색(BFS)
- 현재 위치에서 가장 가까운 노드부터 방문하고 다음 노드로 넘어감
- 모든 노드를 방문할 때 까지 위 과정 반복
✅ 깊이 우선 탐색 구현하기
- 계속해서 깊이 탐색할 수 있어야 함
- 더 이상 깊은 곳이 없는 경우, 가장 최근에 방문했던 노드로 돌아감
- 이미 방문한 노드는 중복해서 방문하지 않아야 함
- 가장 최근에 방문했던 노드로 가는 효율적인 방법
- 스택 활용 (LIFO)
- 방문할 노드는 push , 방문한 노드는 pop . 스택의 top 은 가장 최근에 방문한 노드
- 함수의 call stack 도 stack 과 같이 동작하므로 재귀함수로 구현하는 경우가 많음
- visited 배열을 활용해서 방문 여부를 확인 후 방문함
- 스택 활용 (LIFO)
✅ 너비 우선 탐색 구현하기
- 루트노드부터 시작해서, 가장 가까운 노드들부터 방문할 수 있어야 함
- 루트노드 방문 -> 1개 간선으로 갈 수 있는 노드 방문 -> 2개 간선으로 갈 수 있는 노드 방문 ... (모든 노드를 방문할 때 까지 반복)
- 가장 가까운 노드부터 방문하는 효율적인 방법
- 큐 활용 (FIFO)
- 시작 노드 push
- pop 후에 방문 처리 이후, 현재 노드에서 연결된 노드 중 방문하지 않은 노드 모두 push
- 모든 노드를 방문할 때 까지 2. 번 반복
- 큐 활용 (FIFO)
✅ 깊이 우선 탐색 vs 너비 우선 탐색
- 백트래킹은 깊이우선 탐색에만 존재
- 너비우선탐색으로 찾은 해만 최적해를 보장
- 너비우선탐색은 모든 다음노드를 큐에 푸시하므로 깊이우선탐색보다 메모리 사용량이 높음
- 애매하면 깊이우선탐색 먼저 시도
[참고 강의]
코딩테스트 합격자 되기 - C++ [ https://inf.run/t92e1 ]
[참고 도서]
코딩테스트 합격자 되기 - 파이썬 편